What is Fibonacci Sequence? Why is it important, its Formula and examples?

The Fibonacci sequence is everywhere. We see it in nature, art, and even the stock market. It is a special pattern of numbers that has fascinated people for centuries. It starts with 0 and 1, and each new number is the sum of the two before it.

This sequence was introduced to the world by Leonardo Fibonacci, an Italian mathematician, in the 13th century. He found it while studying how rabbits multiply. But this pattern is not just about rabbits. We find it in sunflower seeds, pinecones, hurricanes, and even galaxies.

Mathematicians use Fibonacci numbers to solve problems. Traders use them to predict stock movements. Designers use them to create beautiful art. The sequence also connects to the Golden Ratio, which is often linked to perfect proportions.

This article will explore the Fibonacci sequence, its importance, its formula, and real-life examples.

The Fibonacci Sequence

Definition

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It typically starts with 0 and 1. So, it goes: 0, 1, 1, 2, 3, 5, 8, 13, and continues indefinitely.

Explanation of How the Sequence is Formed

To form the Fibonacci sequence, we start with 0 and 1. Then, we add these two numbers to get the next one:

• 0 + 1 = 1
• 1 + 1 = 2
• 1 + 2 = 3
• 2 + 3 = 5
• 3 + 5 = 8

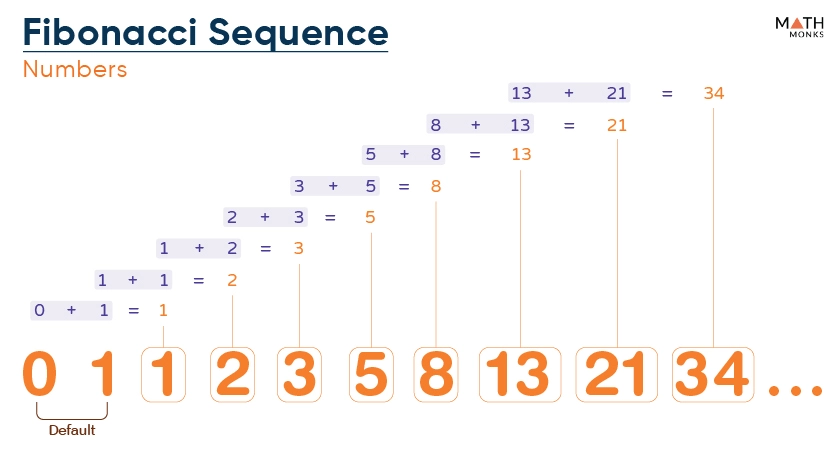
This pattern continues, with each new number being the sum of the two before it.

Mathematical Pattern and Relationship Between Numbers

In mathematical terms, the sequence is defined by the formula:

• F(n) = F(n-1) + F(n-2)

Here, F(n) represents the nth number in the sequence. The relationship between the numbers creates a pattern that appears in various aspects of mathematics and nature.

Importance of Fibonacci Numbers

Role in Mathematics and Number Theory

Fibonacci numbers play a significant role in number theory. They are used in algorithms for tasks like searching and sorting. Additionally, they appear in various mathematical concepts and proofs.

Applications in Computer Science (Data Structures, Algorithms)

In computer science, Fibonacci numbers are used in algorithms and data structures. For example, they are utilized in Fibonacci heaps, which are a type of priority queue that helps improve the efficiency of network optimization algorithms.

Influence in Financial Markets (Fibonacci Retracement in Trading)

Traders use Fibonacci numbers to estimate possible price floors and ceilings in financial markets. This method, known as Fibonacci retracement, involves using horizontal lines to indicate areas where the price might reverse or pause.

Connection to Nature (Spirals in Shells, Flower Petals, Branching in Trees)

Fibonacci numbers appear in various natural patterns:

• Spirals in Shells: The shells of certain mollusks, like the nautilus, follow a spiral pattern that aligns with the Fibonacci sequence.
• Flower Petals: Many flowers have petals in numbers that are Fibonacci numbers, such as lilies with 3 petals or daisies with 34 or 55 petals.
• Branching in Trees: The arrangement of leaves or the branching patterns of some trees follows the Fibonacci sequence, optimizing light exposure and space.

Fibonacci Sequence Formula

Standard Formula: F(n) = F(n-1) + F(n-2), Where F(0) = 0, F(1) = 1

The standard formula for the Fibonacci sequence is:

• F(0) = 0
• F(1) = 1
• F(n) = F(n-1) + F(n-2) for n ≥ 2

This means each number is the sum of the two preceding ones.

Explanation of Recursive and Iterative Approaches

• Recursive Approach: In this method, we define the Fibonacci sequence in terms of itself. For example, to find F(n), we calculate F(n-1) and F(n-2) and add them together. This approach is straightforward but can be inefficient for large n due to repeated calculations.
• Iterative Approach: Here, we start from the base cases (F(0) and F(1)) and build up to F(n) by iteratively computing each subsequent number. This method is more efficient for large n as it avoids redundant calculations.

Binet’s Formula for Direct Computation

Binet’s formula provides a direct way to compute the nth Fibonacci number without calculating all the preceding numbers:

• F(n) = (φ^n – (−φ)^−n) / √5

Here, φ (phi) represents the golden ratio, approximately equal to 1.618.

Examples of Fibonacci Sequence

Calculation of the First 10 Fibonacci Numbers

Let’s calculate the first 10 numbers in the Fibonacci sequence:

1. F(0) = 0
2. F(1) = 1
3. F(2) = F(1) + F(0) = 1 + 0 = 1
4. F(3) = F(2) + F(1) = 1 + 1 = 2
5. F(4) = F(3) + F(2) = 2 + 1 = 3
6. F(5) = F(4) + F(3) = 3 + 2 = 5
7. F(6) = F(5) + F(4) = 5 + 3 = 8
8. F(7) = F(6) + F(5) = 8 + 5 = 13
9. F(8) = F(7) + F(6) = 13 + 8 = 21
10. F(9) = F(8) + F(7) = 21 + 13 = 34

So, the first ten numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.

Simple Example Problems and Solutions

Example 1: Calculate the 7th Fibonacci number.

Solution: Using the sequence, we find F(7) = 13.

Example 2: Find the sum of the first 5 Fibonacci numbers.

Solution: 0 + 1 + 1 + 2 + 3 = 7.

Fibonacci Numbers and the Golden Ratio

The Golden Ratio, symbolized by Phi (φ), is approximately 1.618. It represents a special number where the ratio of two quantities is the same as the ratio of their sum to the larger quantity.

As we progress in the Fibonacci sequence, the ratio of consecutive numbers approaches the Golden Ratio. For example, 21 divided by 13 equals approximately 1.615, close to 1.618.

Applications in Aesthetics, Design, and Nature

• Aesthetics and Design: The Golden Ratio guides the design of visually appealing compositions in art, architecture, and product design.
• Nature: The arrangement of leaves, seeds, and other natural patterns often exhibit the Golden Ratio, reflecting efficiency and harmony.

Closing

The Fibonacci sequence is more than a series of numbers; it’s a pattern deeply embedded in mathematics, nature, and human creations. From the spirals of galaxies to the structure of music, its influence is vast. Understanding this sequence enriches our appreciation of the world’s inherent order and beauty.

Frequently Asked Questions (FAQs)

Disclaimer

The information provided here is for educational purposes and reflects knowledge up to March 2025. For the latest research and applications, please consult current resources.